算法：柱状图中最大的矩形

算法

发布日期: 2020-05-29

题目：柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。求在该柱状图中，能够勾勒出来的矩形的最大面积。

以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

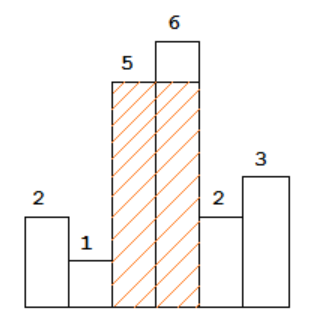
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

输入: [2,1,5,6,2,3]
输出: 10

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/largest-rectangle-in-histogram

分析

拿到这道题，先不要想其他的方法，看看暴力解法能不能算出来。我们会发现暴力算法有两个方案：一个是变化矩形的范围，然后求出范围中的最低柱子，就可以得到面积了。第二个是每个柱子分别向前后扩散，遇到比自己低的就停下来，那么这个范围的宽度乘上自身的高度，就是该位置的柱子可以达到的最大面积。（第二种我当时没想出来==）

然后我们从暴力算法中，看看有没有可以进行优化的地方。首先两种思路，第一种的话因为已经固定了两层嵌套循环，要去优化的话显然有点困难。第二种的思路只有一个外层循环，所以优化的空间可能会比较大，我们从第二种入手。

首先我们知道，第二种思路最费时间的点就是每次都要前后去寻找，那我们这里可以去想一下怎么把前面遍历的情况记录下来，节省时间。所以难点就是在确定边界。

重要特点：这里我们分析边界的特点。如果i < j ,且heights[i] > heights[j] ,这样的话，对于任何 j < k,第K个元素的左边界不可能是i。因为被 j 挡住了。这个应该很好理解吧。可以的话我们继续。

首先我们进行遍历数组，看什么时候可以确定边界。假设现在有[2,4,1,5,7,3]。（大家可以自行画图体验，我这里就不画图了，懒癌犯了）

遍历到2的时候，已经确定好左边界，但是还没有确定右边界；
遍历4，同二。
遍历1，这个时候我们会发现，第二个元素4，已经确定好边界了，可以得出面积4.
然后可以发现第一个元素2，也得到他的边界了。
然后我们会发现，位置1 比前面的任何元素都要小，那么后面的元素，不可能以2,4为左边界。原因看上面。
然后同理继续遍历5，和7.然后遍历到3的时候，元素 7 也确定边界了。元素5也确定边界了。
后面已经没有元素了，所以3也可以确定边界。最后再确定1的边界。

观察上面的流程，有没有一丝丝什么的味道？栈的味道。遍历可以看做是入栈，确定边界的时候，可以看成出栈。先进后出。那么可不可以用一个辅助栈来完成这个流程呢？答案是肯定的。

思路和上面一模一样，重点是入栈和出栈。从上面的重要特点可以知道，当遇到比较小的元素的时候，那么前面的元素就可以确定边界了，进行出栈操作。所以栈底，永远是前面的最小元素。

当遍历到的元素比栈顶要小的时候，那么就可以对栈顶元素进行出栈
这个矩形的高度是栈顶元素的高度，宽度是当前遍历到的元素的下标 i - 栈顶元素的下一个元素的下标 j + 1.为什么是这样？大家可以画个图模拟一下，就留给大家思考了。
遍历完成后，再对栈里的元素进行出栈操作。
过程中记录最大的矩形面积。

这里建议大家画图去模拟这个过程，会很好去理解，特别是关于矩形的边界的确定，如果没有画图，很容易就漏掉一些细节的考虑。

代码实现

public static int largestRectangleArea(int[] heights) {
    if (heights.length==0) return 0;
    Stack<Integer> stack = new Stack<>();
    stack.push(0);
    int maxArea = 0;
    for (int i=1;i<heights.length;i++){
        if (heights[i]>=heights[stack.peek()]) stack.push(i);
        else {
            while (!stack.isEmpty() && heights[i]<heights[stack.peek()] ){
                int index = stack.pop();
                int area;
                if (stack.isEmpty()){
                    area = i*heights[index];
                }else{
                    area = (i-stack.peek()-1)*heights[index];
                }
                maxArea = Math.max(maxArea, area);
            }
            stack.push(i);
        }
    }
    while (!stack.isEmpty()){
        int index = stack.pop();
        int area;
        if (stack.isEmpty()){
            area = heights.length*heights[index];
        }else{
            area = (heights.length-stack.peek()-1)*heights[index];
        }
        maxArea = Math.max(area,maxArea);
    }
    return maxArea;
}